修改Cauchy-Goursat定理的证明
最近冒出个点子，需要把复分析里的一些结论做一个推广1。然而Couchy-Goursat定理的原证明并不能直接进行推广，于是我修改了一下证明。
先放上原证明：
Cauchy-Goursat 积分定理
设 $f(z)$ 是单连通区域 $D$ 内的解析函数. 若 $L$ 是 $D$ 内任一条简单曲线, 取逆时针方向, 则
修改：
1.把引理中 $\eta$ 的定义换成 $0<\eta\le\min{\delta,\delta’}$ ，于是让 $\eta$ 趋于0——即n趋于无穷——也有
\[\left|\int_{L} f(z) \mathrm{d} z-\int_{P} f(z) \mathrm{d} z\right|<\varepsilon\]即
\[\int_{L} f(z) \mathrm{d} z=\int_{P} f(z) \mathrm{d} z\]2.补充一下引理证明第一段里最后一句“完全在G内”的证明。
$\forall p\in\partial G$，可构造三角形 $pz_kz_{k-1}$ ，其中 $pz_k\ge\delta’,pz_{k-1}\ge\delta’$ 。 由于三角形的顶点和对边不相交，因此得证。
3.修改证明后半部分，即三步中的后两步。这部分可以说是完全换了个思路。
首先我们有任意的一条路径 $L$ ，在 $L$ 上取点 $z_0,z_1,z_2,\cdots ,z_{2^n}$，使每个弧段 $z_{k-1}z_k$ 长度小于 $\eta$ 。对于所有的 $a$ 从0到n，连结所有下标为 $2^{n-a}m\,\,\,(m=0,1,2\cdots)$ 的点，得到的折线记为 $P_a$ 。
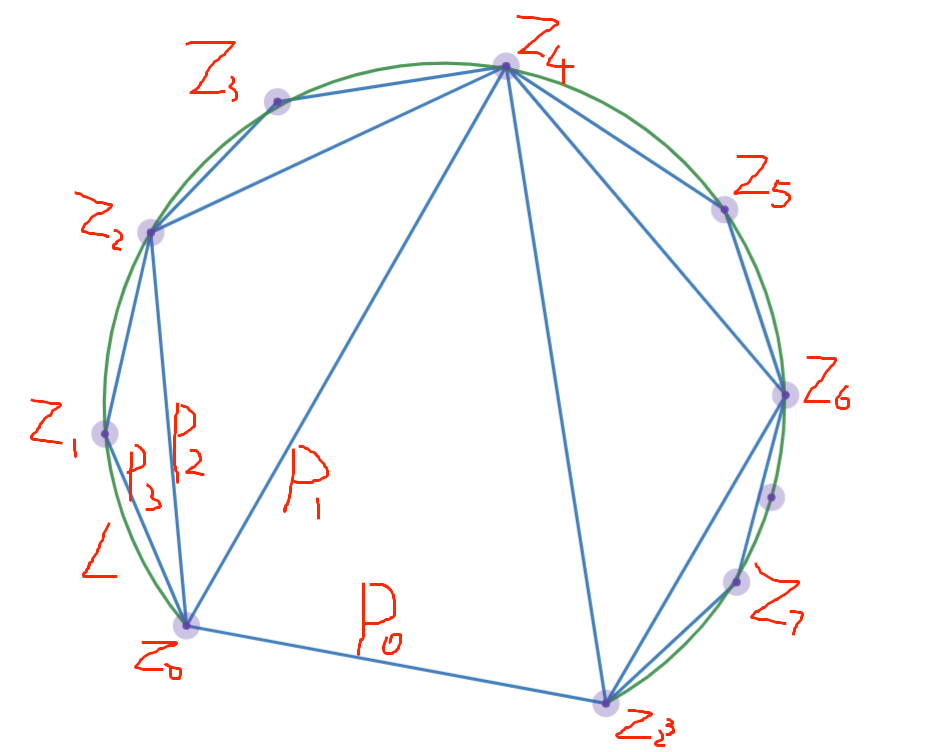
注意 以上这一步不再对所有区域 $D$ 有效了。比较保守的话，可以让 $D$ 是有界凸集或者全集。我初想到这一点的时候也很惋惜。
对于每个相邻的 $P_{k-1},P_k$ ，它们组成了一组三角形的边界。一看到三角形，自然想到第一步里的结论。于是如果让积分方向为顺下标方向（如z0-z1-z2-z0），那么易知
\[\int_{P_k} f(z) \mathrm{d} z=\sum_{\bigtriangleup }\int_{\partial \bigtriangleup } f(z) \mathrm{d} z+\int_{P_{k-1}} f(z) \mathrm{d} z\]由第一步里的结论已知
\[\int_{\partial \bigtriangleup } f(z) \mathrm{d} z=0\]于是
\[\int_{P_k} f(z) \mathrm{d} z=\int_{P_{k-1}} f(z) \mathrm{d} z\]进而对于任意两个 $P_{i},P_j$ ，有
\[\int_{P_i} f(z) \mathrm{d} z=\int_{P_{j}} f(z) \mathrm{d} z\]而在修改1里已证明
\[\int_{L} f(z) \mathrm{d} z=\lim_{i\to\infty}\int_{P_i} f(z) \mathrm{d} z\]所以
\[\int_{L} f(z) \mathrm{d} z=\int_{P_0} f(z) \mathrm{d} z\]也就证明了积分的值和路径无关，只和起点终点有关。于是可以取起点=终点，就证明了弱的 Cauchy-Goursat 积分定理。